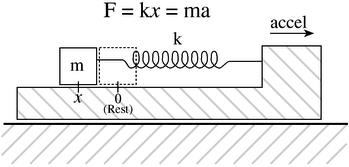
Figure 8: Mass-Spring system used for measuring acceleration
The basic physical principle behind this accelerometer (as well as many others), is that of a simple mass spring system. Springs (within their linear region) are governed by a physical principle known as Hooke's law. Hooke's law states that a spring will exhibit a restoring force which is proportional to the
amount it has been stretched or compressed. Specifically, F=kx, where k is the constant of proportionality between displacement (x) and force (F). The other important physical principle is that of Newton's second law of motion which states that a force operating on a mass which is accelerated will exhibit
a force with a magnitude F=ma. Figure 8 shows a mass connected to a spring. If this system undergoes an acceleration, then by Newton's law, there will be a resultant force equal to ma. This force causes the mass to either compress or expand the spring under the constraint that F=ma=kx.
Hence an acceleration a will cause the mass to be displaced by 
or alternatively, if we observe a displacement of x, we know that the mass has undergone an acceleration of 
. In this way we have turned the problem of measuring acceleration into one of measuring the displacement
of a mass connected to a spring. Note that this system only responds to accelerations along the length of the spring. This is said to be a single axis accelerometer. In order to measure multiple axes of acceleration, this system needs to be duplicated along each of the required axes.
Figure 9: Mass-spring system used in the Analog Devices ADXL50 accelerometer
The Analog Devices ADXL50 is a micro-machined stand-alone accelerometer which consists of a mass spring system as well as a system to measure displacement and the appropriate signal conditioning circuitry (which is the topic of the next section). The mass spring system used in this device is depicted in Figure 9. The mass is a bar of silicon, and the spring system is implemented by the 4 tethers which attach to each corner of the mass. It responds to accelerations that occur in line with the length of the mass. When an acceleration occurs, the mass moves with respect to the anchored ends of the tethers. Roughly speaking, the amount of acceleration is proportional to the amount of displacement of the mass. This is not quite true in this case since the spring system is not an ideal spring as presented earlier. This fact is compensated for by some sophisticated signal conditioning circuitry present in the device.
Figure 10: A simple capacitor
The next problem which needs to be solved is that of measuring the displacement of the bar. The principle upon which this is based is that of the electrical property of capacitance. Capacitors are electrical components which store charge. A simple capacitors is formed by placing two metal plates in parallel
with each other as shown in Figure 10. The amount of capacitance that a device such as this would exhibit is exhibit is given by 
, where k is a property of the material between
the two plates. Using this, if one knew k and could measure capacitance, they would be able to determine 
, the spacing between the plates.
Figure 11: The dual Capacitor system used to measure displacement in the Analog Devices ADXL50 accelerometer
The ADXL50 takes this technique one step further and uses two capacitors configured as in Figure 11. If the device is at rest, and the spacing between each of the plates is , then each of the
capacitors exhibits a capacitance of . If the middle plate is moved by a distance x, then this results in:
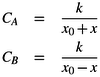
This can then be written as:
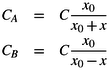
The ADXL50 measures the difference between the two capacitors which is given by:
For small values of displacement x, the above expression reduces to:
Hence the difference in capacitance is proportional to x, but only for small values of displacement. The ADXL50 uses a negative feedback control loop to make sure that the movement of the mass is kept small so that the above expression remains correct. Figure 12 shows a block diagram of the entire system.
Figure 12: Block diagram of the Analog Devices ADXL50 accelerometer
