Human Computer Interface Technology
Physics Review Lecture
September 25, 2002
Perry R. Cook,
Princeton University
Basic Newtonian Physics
Position and its derivatives
Position as function of time:

- Velocity as function of time is rate of change of Position with respect to time.
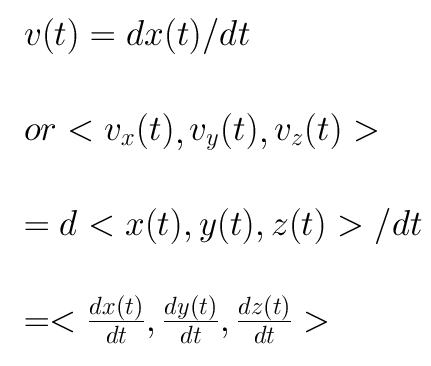
- Acceleration as function of time is rate of change of Velocity with respect to time.

Units: m (meters) and s (seconds)
- Position: m
Velocity: m/s
Acceleration: m/s/s = m/s^2
Force
- Force: F = ma (Newton's 2nd Law (with m = constant))

- Acceleration due to gravity, at sea level, on earth, is:

- Force due to gravity (sea level, earth) is: mg Newtons
- Frictional Forces:
- When stationary, the coefficient of static friction is:

- When moving, the coefficient of kinetic friction is:

- Force due to friction acts opposite other forces,
and is equal to

Example:
- When stationary, the coefficient of static friction is:


Energy (work) and Energy Flow
- Energy: W = F x (force through a distance, if F is constant)

- Power: = Energy flow, or the time rate of work = dW(t)/dt

- Potential Energy: Potential to do work because of position in a field
- In a conservative field, potential (and work)
only depends on
initial and final positions, not on path or time taken to traverse it.Example: Gravitational Potential Energy =

- Kinetic Energy: Ability to do work because of mass
in motion

Note that Kinetic Energy being related to the square of the velocity means that stopping a car takes four times the distance (constant frictional forces) if the car is going twice as fast.
- Energy is Conserved, A Very Important Physical Concept!!!
Example: Potential and Kinetic energy, dropping a ball
Initial Potential + Initial Kinetic = Final Potential + Final Kinetic

Mass cancels!! (Galileo and later some moon-walkers proved this experimentally)
- Mass is Conserved, Another Very Important Physical Concept!!!
Example: If I pound water into a hose, it either comes out the other
end or the hose eventually blows up. Mass is conserved.
Rotational Frames of Reference
- All of the above still works, just adjusted slightly

Example: A fulcrum with a pivot at 1/3 its length will balance with
twice as much mass on the short end as on the long end.Assume it's balanced and at rest (acceleration = 0)

- Rotational Energy:

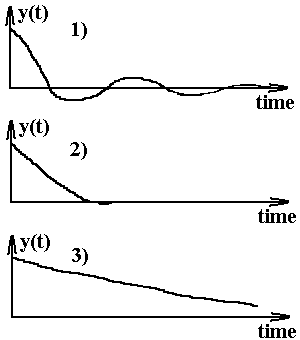
The Basic 2nd Order Mechanical System
A spring with constant k (Force = -k y)
A mass with mass m
Some oil with damping R (Force = -R v)
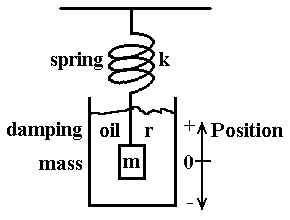
y is the signed displacement from equilibrium (at rest with y = 0).
Minus sign on spring term means force acts to restore mass to rest position.
Minus sign on damping term means force acts against motion,
proportional to velocity.
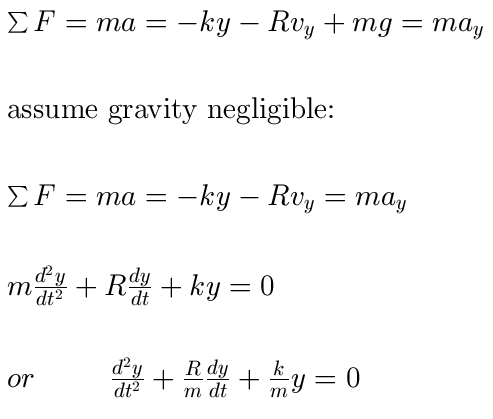
Solutions:
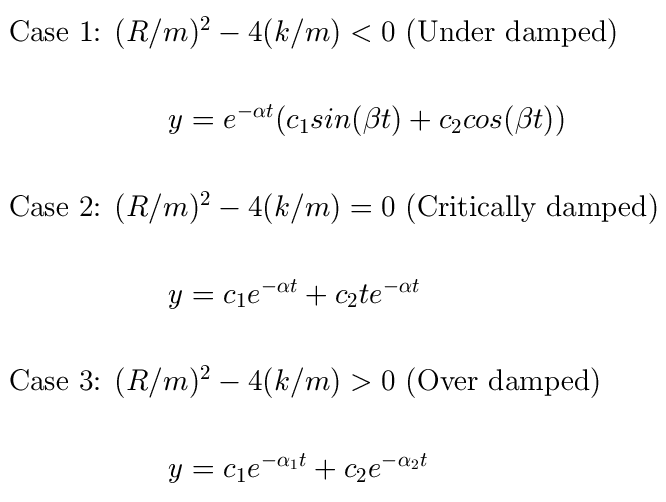
* Permission to make digital or hard copies of part or all
of this work for personal or classroom use is granted with
or without fee provided that copies are not made or dis-
tributed for profit or commercial advantage and that copies
bear this notice and full citation on the first page. To copy
otherwise,to republish, to post on services, or to redistribute
to lists, requires specific permission and/or a fee.