

Next: 5.2 Sample and Hold
Up: 5 Data Acquisition
Previous: 5 Data Acquisition
The Nyquist criterion dictates that all signals must be bandlimited to less than half the
sampling rate of the sampling system. Many signals already have a limited spectrum, so
this is not a problem. However, for broad spectrum signals, an analog lowpass filter must
be placed before the data acquisition system. The minimum attenuation of this filter at the
aliasing frequency should be at least:
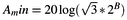 where B is the number of bits of the ADC. This formula is derived from the fact that there
is a minimum noise level inherent in the sampling process and there is no need to attenuate
the sensor signal more than to below this noise level.
where B is the number of bits of the ADC. This formula is derived from the fact that there
is a minimum noise level inherent in the sampling process and there is no need to attenuate
the sensor signal more than to below this noise level.
- Time Response: In designing an anti-aliasing filter, there is a temptation to have it's
attenuation roll-off extremely quickly. The way to achieve this is to increase the order
of the filter (see the previous discussion of filter order). A so-called brick-wall filter
(one with infinitely high order), however, causes a sinc function time response that
decays proportionally to 1/t. What this means is that an extremely high order filter that
eliminates all signals above the cutoff frequency will cause signals that change rapidly
to ring on for a long time. A very undesirable effect.
- Phase Distortion / Time delay: Most analog filters have a non-linear phase response.
This a problem since non-linear phase causes an unequal time (group) delay as a
function of frequency. The higher frequency signals will arrive later than low frequency
signals. This can especially be a problem when multiple sensor outputs are compared
such as when using a microphone array.
- Amplitude Distortion: By definition, the filter will modify the frequency structure of
the sensor signal which is usually not desired
- Increase the sampling rate of the ADC. This allows the antialiasing filter to have a
higher cutoff frequency and still eliminate aliasing. This enables the following:
- The filter rolloff can be more shallow - allowing a better time response
- The frequency response of the filter does not attenuate the lower sensor
frequencies of interest
- Phase distortion is strongest around the cutoff frequency of the filter so if
this is pushed higher, it will not affect the sensor frequencies this cutoff
- Have linear phase filters. This, of course, will reduce the phase distortion
problems.


Next: 5.2 Sample and Hold
Up: 5 Data Acquisition
Previous: 5 Data Acquisition
Tim Stilson
Thu Oct 17 16:32:33 PDT 1996
![]() where B is the number of bits of the ADC. This formula is derived from the fact that there
is a minimum noise level inherent in the sampling process and there is no need to attenuate
the sensor signal more than to below this noise level.
where B is the number of bits of the ADC. This formula is derived from the fact that there
is a minimum noise level inherent in the sampling process and there is no need to attenuate
the sensor signal more than to below this noise level.